高中数学知识点:反函数
逍遥右脑 2017-07-02 18:21
定义:
设式子y=f(x)表示y是x的函数,定义域为A,值域为C,从式子y=f(x)中解出x,得到式子x= (y),如果对于y在C中的任何一个值,通过式子x=
(y),如果对于y在C中的任何一个值,通过式子x= (y),x在A中都有唯一确定的值和它对应,那么式子x=
(y),x在A中都有唯一确定的值和它对应,那么式子x= (y)就表示y是x的函数,这样的函数叫做y=f(x)的反函数,记作x=f-1(y),即x=
(y)就表示y是x的函数,这样的函数叫做y=f(x)的反函数,记作x=f-1(y),即x= (y)=f-1(y),一般对调x=f-1(y)中的字母x,y,把它改写成y=f-1(x)。
(y)=f-1(y),一般对调x=f-1(y)中的字母x,y,把它改写成y=f-1(x)。
反函数的一些性质:
(1)反函数的定义域和值域分别是原函数的值域和定义域,称为互调性;
(2)定义域上的单调函数必有反函数,且单调性相同(即函数与其反函数在各自的定义域上的单调性相同),对连续函数而言,只有单调函数才有反函数,但非连续的非单调函数也可能有反函数;
(3)函数y=f(x)的图象与其反函数y=f-1(x)的图象关于直线y=x对称,但要注意:函数y=f(x)的图象与其反函数x= (y)=f-1(y)的图象相同。(对称性)
(y)=f-1(y)的图象相同。(对称性)
(4)设y=f(x)与y=g(x)互为反函数,如果点(a,b)在函数y=f(x)的图像上,那么点(b,a)在它的反函数y=g(x)的图像上。
(5)函数y=f(x)的反函数是y=f-1(x),函数y=f-1(x )的反函数是y=f(x),称为互反性,但要特别注意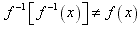 ;
;
(6)函数y=f(x)的图象与其反函数y=f-1(x)的图象的交点,当它们是递增时,交点在直线y=x上。当它们递减时,交点可以不在直线y=x上,
如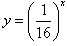 与
与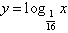 互为反函数且有一个交点是
互为反函数且有一个交点是 ,它不再直线y=x上。
,它不再直线y=x上。
(7)还原性: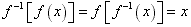 。
。
求反函数的步骤:
(1)将y=f(x)看成方程,解出x=f-1(y);
(2)将x,y互换得y =f-1(x);
(3)写出反函数的定义域(可根据原函数的定义域或反函数的解析式确定);
另外:分段函数的反函数可以分别求出各段函数的反函数再合成。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容,请发送邮件至 lxy@jiyifa.cn 举报,一经查实,本站将立刻删除。