高中物理知识点:碰撞
逍遥右脑 2018-08-26 15:31
1、特点:
①时间:过程持续时间即相互作用时间极短
②作用力:在相互作用的过程中,相互作用力先是急剧增大,然后再急剧减小,平均作用力很大
③动量守恒条件:系统的内力远远大于外力,所以,系统即使所受外力之和不为零,外力也可以忽略,系统的总动量守恒
④位移:碰撞过程是在一瞬间发生的,时间极短,所以,在物体发生碰撞的瞬间,可忽略物体的位移,可以认为物体在碰撞前后仍在同一位置
⑤能量:在碰撞过程中,一般伴随着机械能的损失,碰撞后系统的总动能要小于或等于碰撞前系统的总动能,
2、两物体相碰通常有以下三种情况
①两物体碰撞后,动能无损失,称为弹性碰撞。当两相等质量的物体发生弹性碰撞时,则发生速度交换,这是一个很有用的结论。
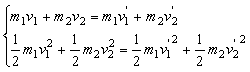
②两物体碰撞后虽分开,但动能有损失,称为非弹性碰撞。
③两物体碰撞后合为一个整体,以某一共同速度运动,称为完全非弹性碰撞。此类碰撞中动能损失最多,即动能转化为其他形式能的值最多。
弹性碰撞及讨论:
质量为m1与质量为m2的物体分别以速度 运动并发生对心碰撞,碰撞过程中无机械能损失(如图所示)。
运动并发生对心碰撞,碰撞过程中无机械能损失(如图所示)。
设碰后两物体的速度分别为
据动量守恒得
据机械能守恒得
由①②两式得
由上述表达式可以看出:
(1)若
(2)若 即速度交换。
即速度交换。
(3)若 ,即m2的速度几乎不变。
,即m2的速度几乎不变。
“一动一静”模型:
(1)弹性正碰,如图所示,在光滑水平面上质量为 m1的小球以速度v1与质量为m2的静止小球发生弹性正碰.
讨论碰后两球的速度 根据动量守恒和机械能守恒有:
根据动量守恒和机械能守恒有:
解上面两式可得:
碰后m1的速度
碰后m2的速度
讨论:
①若表示
 表示m1的速度不变,m2以2v1速度被撞出去。
表示m1的速度不变,m2以2v1速度被撞出去。
②若 都是正值,表示
都是正值,表示 都与v1方向相同。
都与v1方向相同。
③若 ,则有即碰后两球速度互换。
,则有即碰后两球速度互换。
④若 为负值,表示
为负值,表示 方向相反, m1被弹回。
方向相反, m1被弹回。
⑤若 这时
这时
 表示m1被反向以原速率弹回,而m2仍静止。
表示m1被反向以原速率弹回,而m2仍静止。
⑥
两物体碰后的速度随两物体的质量比变化情况如图所示。 
⑦能量传递:在弹性碰撞中,传递的能量跟两者质量比 有关,即
有关,即
 两球质量越接近,碰撞中传递的动能越大;在
两球质量越接近,碰撞中传递的动能越大;在 两种情况下,传递的动能相等。
两种情况下,传递的动能相等。
(2)完全非弹性碰撞上例中m1与m2发生完全非弹性碰撞,则有
 ,碰后的共同速度
,碰后的共同速度
损失的动能
“二合一”模型:
这种模型是指两个速度不同的物体通过发生相互作用,最终两物体粘在一起运动或以共同的速度运动的模型。
这种模型的主要特征是终态共速(也可以是只在某一时刻共速.而研究的过程是从初始到共速的过程),从能量角度来看,这种过程中能量损失是最大的,属于完全非弹性碰撞的类型,在一维碰撞中的方程有:
相互作用的两个物体在很多情况下皆可当成碰撞处理,那么对相互作用中两物体相距“恰最近”、相距 “恰最远”或“恰上升到最高点”等一类,临界问题,求解的关键都是“速度相等”。在“类碰撞”问题中,碰撞时间不一定很短,但遵守的规律却是相同的,例如下面几种情形。
(1)如图中,光滑水平面上的A物体以速度v0去撞击静止的B物体,A、B两物体相距最近时,两物体速度必定相等,此时弹簧最短,其压缩量最大,系统损失的动能等于弹簧获得的弹性势能, 
(2)在图中,物体A以速度v0滑到静止在光滑水平面上的小车B上,当A在B上滑行的距离最远时,A、B相对静止,A、B的速度必定相等,系统损失的动能等于AB间摩擦产生的热量。 
(3)在图中,子弹以速度v0射入静止在光滑的水平面上的木块中。当子弹不穿出时,子弹和木块的速度必定相等,系统损失的动能等于子弹与木块间摩擦产生的热量。 
(4)如图所示,质量为M的滑块静止在光滑水平面上,滑块的光滑弧面底部与桌面相切,一个质量为m 的小球以速度v0向滑块滚来。设小球不能越过滑块,则小球到达滑块上的最高点时(即小球在竖直方向上的速度为零),两者的速度肯定相等(方向为水平向右),小球获得的重力势能等于系统损失的动能
碰撞合理性的判断方法:
碰撞的合理性要遵循动量守恒定律、能量关系和速度关系:
1.系统动量守恒
2.碰撞过程中系统的总动能不会增加
如果物体发生的是弹性碰撞,总动能不变;其他情况碰撞后会有部分动能转化为内能,系统的动能将减小。即 
3.速度要符合情景如果碰前两物体同向运动,则后面物体的速度必大于前面物体的速度,即 否则无法实现碰撞。碰撞后,原来在前的物体速度一定增大,且原来在前的物体速度大于或等于原来在后的物体速度,即
否则无法实现碰撞。碰撞后,原来在前的物体速度一定增大,且原来在前的物体速度大于或等于原来在后的物体速度,即
 否则碰撞没有结束。如果碰前两物体是相向运动,则碰后,两物体的运动方向不可能都不改变,除非两物体碰撞后速度均为零。
否则碰撞没有结束。如果碰前两物体是相向运动,则碰后,两物体的运动方向不可能都不改变,除非两物体碰撞后速度均为零。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容,请发送邮件至 lxy@jiyifa.cn 举报,一经查实,本站将立刻删除。